백준 10058번 센서 네트워크

문제 링크

정답인 집합 $s$를 생각하자. $s$에서 가장 먼 두 점을 $a, b$와 그 거리를 $d$라고 하자.

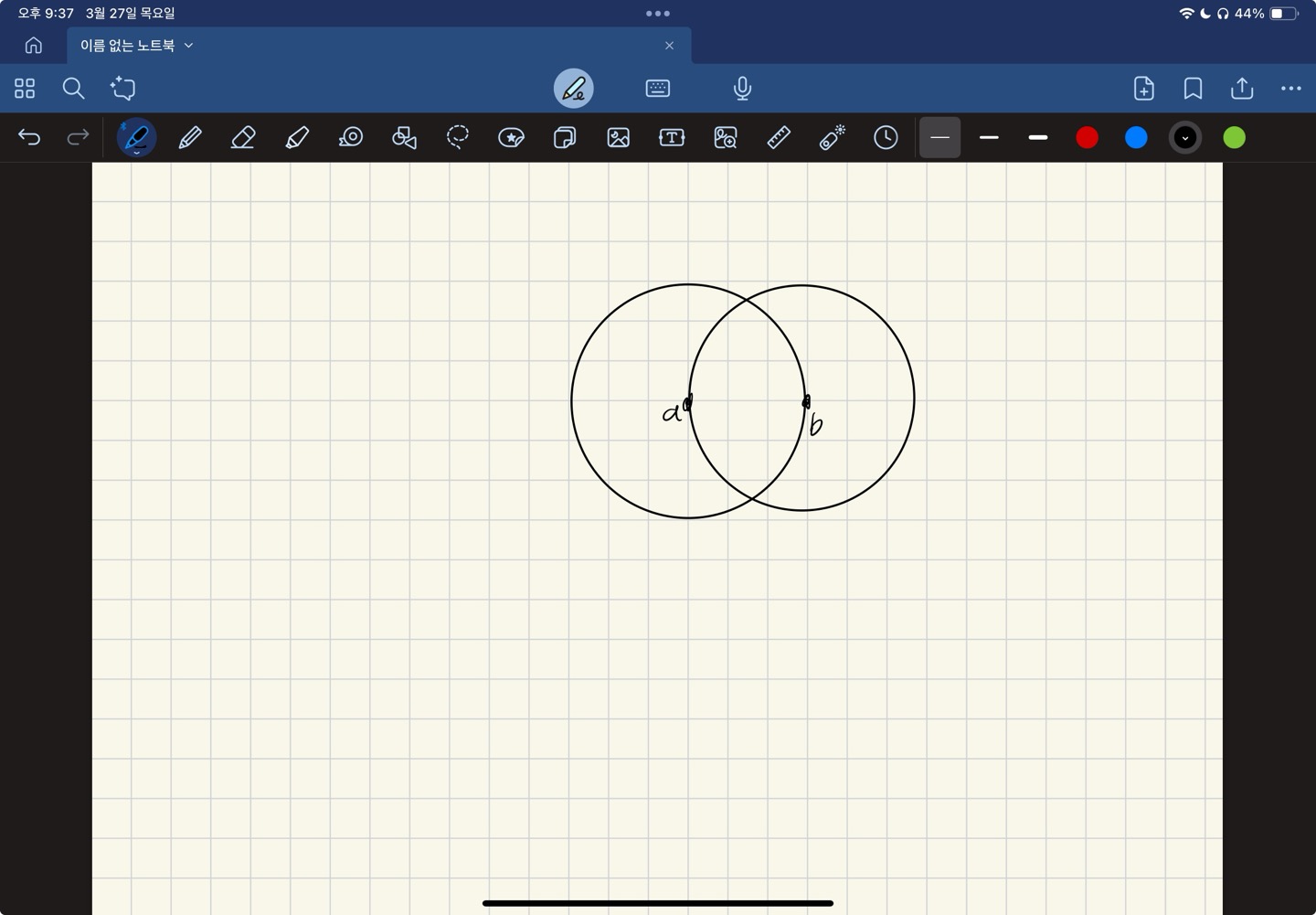
$a, b$를 중심으로 하고 반지름이 $d$인 두 원을 생각하자.

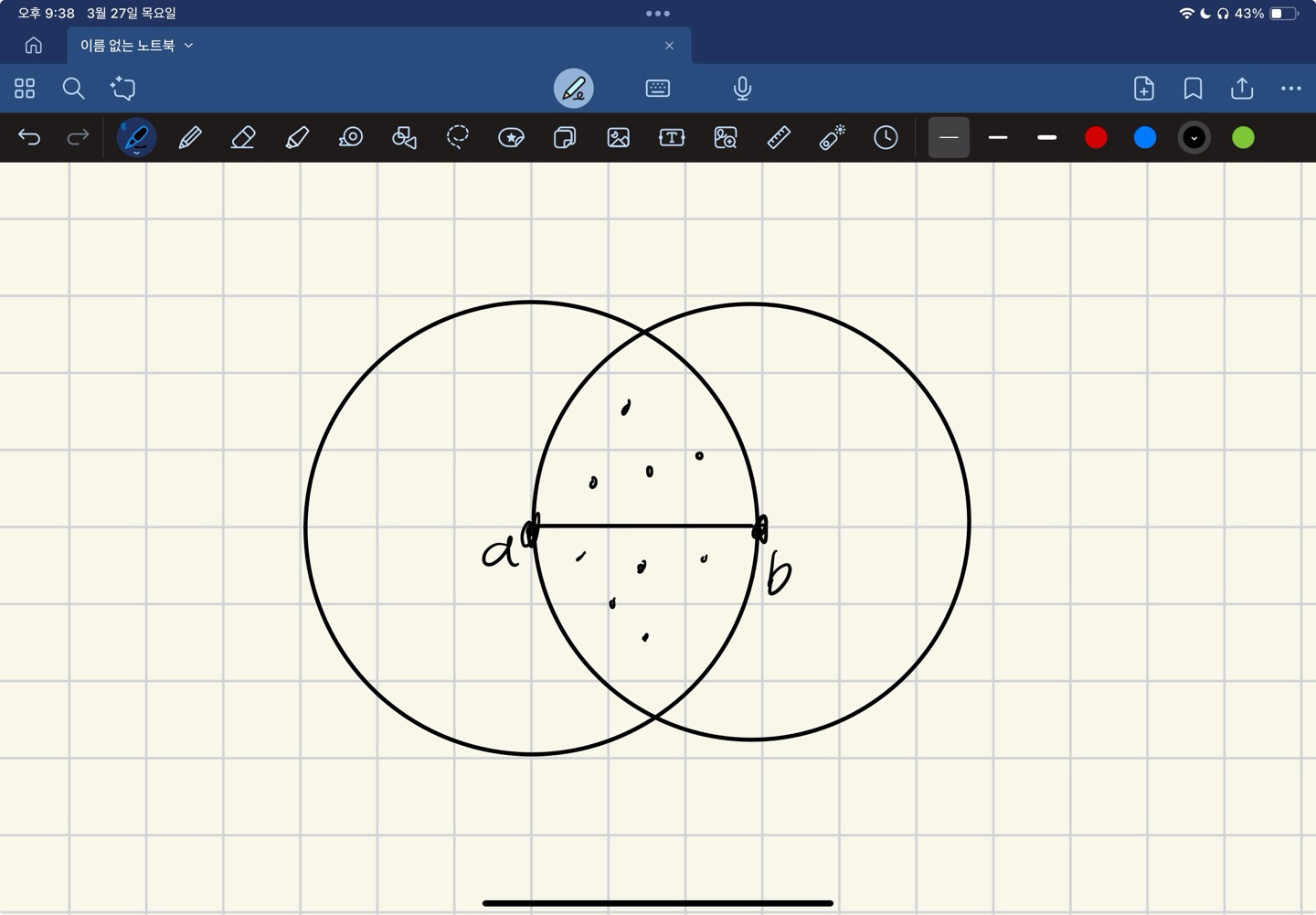
$a, b$가 가장 먼 두 점이기 때문에 두 원이 겹치는 영역안에 집합의 모든 점이 들어갈 수 있다. 선분 $\overline{ab}$을 기준으로 두 구역 $p, q$로 나누자. 같은 구역에 있는 점은 거리가 $d$이하이다.

만약 집합이 올바른 정답이려면 $p$의 한 점과 $q$의 한 점의 거리는 $d$이하이다.

그러면 원래 문제로 돌아오자.

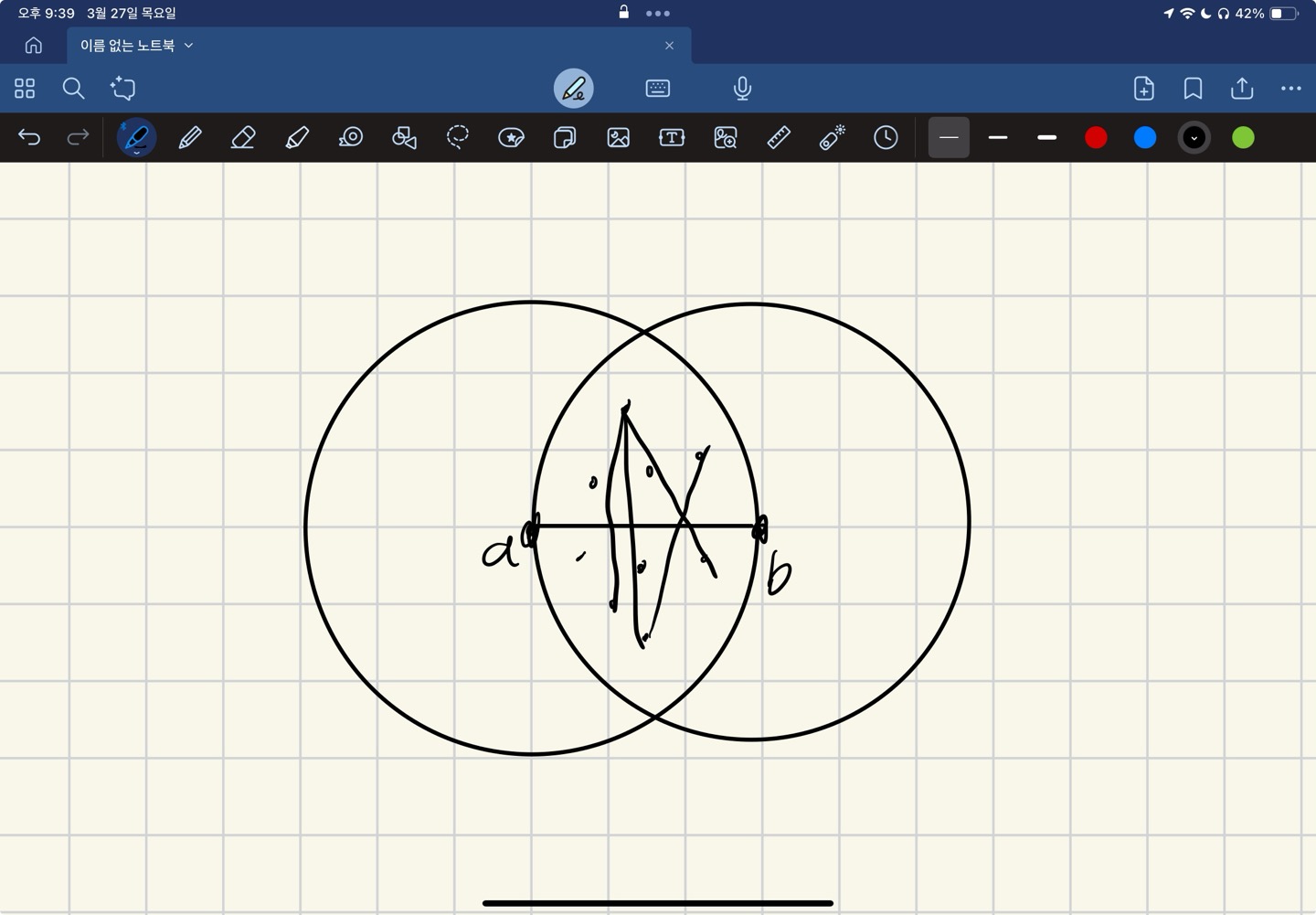
임의의 두 점 $a, b$를 고정하자. $a, b$ 사이 거리를 $d$라고 하고 $a, b$와의 거리가 $d$이하인 점만 보자. 점을 $\overline{ab}$ 기준으로 두 구역 $p, q$로 나누자.

$p$의 한 점과 $q$의 한 점 사이 거리가 $d$이상이라면 두 점에 간선을 잇자. 그렇게 나온 그래프는 이분그래프이다. 정점을 적당히 지워서 모든 간선을 지울 수 있다면 $a, b$를 가장 먼 점으로 가지는 정답 후보를 찾을 수 있다. 문제가 minimum vertex cover문제로 환원되었다. 지울 정점은 이분매칭을 통해 구할 수 있다.

#include <bits/stdc++.h>

using namespace std;

const int MAXN = 105;

bool vst[MAXN], coverB[MAXN];
int N, d, X[MAXN], Y[MAXN], owner[MAXN], rowner[MAXN];
vector<int> graph[MAXN];

int ccw(int x1, int y1, int x2, int y2, int x3, int y3)
{
    return (x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1);
}

int dist(int x1, int y1, int x2, int y2)
{
    int x = x1 - x2;
    int y = y1 - y2;
    return x * x + y * y;
}

bool dfs(int u)
{
    for(auto v : graph[u]) {
        if(vst[v]) continue;
        vst[v] = true;
        if(owner[v] == -1 || dfs(owner[v])) {
            owner[v] = u;
            rowner[u] = v;
            return true;
        }
    }
    return false;
}

void dfs2(int u)
{
    vst[u] = true;
    for(auto v : graph[u]) {
        coverB[v] = true;
        if(!vst[owner[v]]) dfs2(owner[v]);
    }
}

vector<int> solve(int i, int j)
{
    vector<int> up, dw;
    int r = dist(X[i], Y[i], X[j], Y[j]);
    for(int k = 1; k <= N; k++) {
        if(dist(X[i], Y[i], X[k], Y[k]) <= r && dist(X[j], Y[j], X[k], Y[k]) <= r) {
            if(ccw(X[i], Y[i], X[j], Y[j], X[k], Y[k]) >= 0)
                up.push_back(k);
            else
                dw.push_back(k);
        }
    }

    memset(owner, -1, sizeof(owner));
    memset(rowner, -1, sizeof(rowner));
    for(int k = 1; k <= N; k++) {
        graph[k].clear();
    }

    for(auto u : up) {
        for(auto d : dw) {
            if(dist(X[u], Y[u], X[d], Y[d]) > r) {
                graph[u].push_back(d);
            }
        }
    }

    for(auto u : up) {
        memset(vst, 0, sizeof(vst));
        dfs(u);
    }

    vector<int> ans;
    memset(vst, 0, sizeof(vst));
    memset(coverB, 0, sizeof(coverB));
    for(auto u : up) {
        if(rowner[u] == -1) dfs2(u);
    }

    for(auto u : up) {
        if(rowner[u] == -1 || vst[u]) ans.push_back(u);
    }
    for(auto d : dw) {
        if(!coverB[d]) ans.push_back(d);
    }

    sort(ans.begin(), ans.end());

    return ans;
}

signed main()
{
    cin >> N >> d;
    d = d * d;
    for(int i = 1; i <= N; i++) {
        cin >> X[i] >> Y[i];
    }

    vector<int> ans = {1};
    for(int i = 1; i <= N; i++) {
        for(int j = 1; j < i; j++) {
            if(dist(X[i], Y[i], X[j], Y[j]) <= d) {
                auto cand = solve(i, j);
                if(cand.size() > ans.size()) {
                    ans = cand;
                }
            }
        }
    }

    cout << ans.size() << "\n";
    for(auto i : ans) cout << i << " ";
}